假设检验的原理
假设检验的概念
- 对总体的参数或分布形态做出一个假设,然后利用样本的信息来判断假设是否合理,从而决定是否接受所做出的假设。
- 参数检验 总体形态已知,需要对总体的未知参数进行检验。
- 非参数检验 对总体分布形态所知较少,对未知分布函数的形式及其他特征进行检验。
假设
- H1 希望得到证实的假设,又称备择假设、研究假设、科学假设或对立假设
- H0 直接被检验的假设,又称虚无假设、无差假设、零假设或原假设
反证法
- 为了检验H1,首先需要假设H0为真
- 若出现“不合理现象”,则不能接受H0,转而接受H1
- 若没有出现“不合理现象”,接受H0,拒绝H1
小概率事件
- 在心理学实验中,“不合理现象”指小概率事件在一次试验中发生。
- 通常将发生概率不超过0.05或0.01的事件称为“小概率事件”。
我们将这个概率称为显著性水平,并用表示。
结合反证法,表述为
- 如果某个事件的发生概率不超过0.05或0.01,则拒绝H0,接受H1
- 如果某个事件的发生概率超过0.05或0.01,则接受H0,拒绝H1
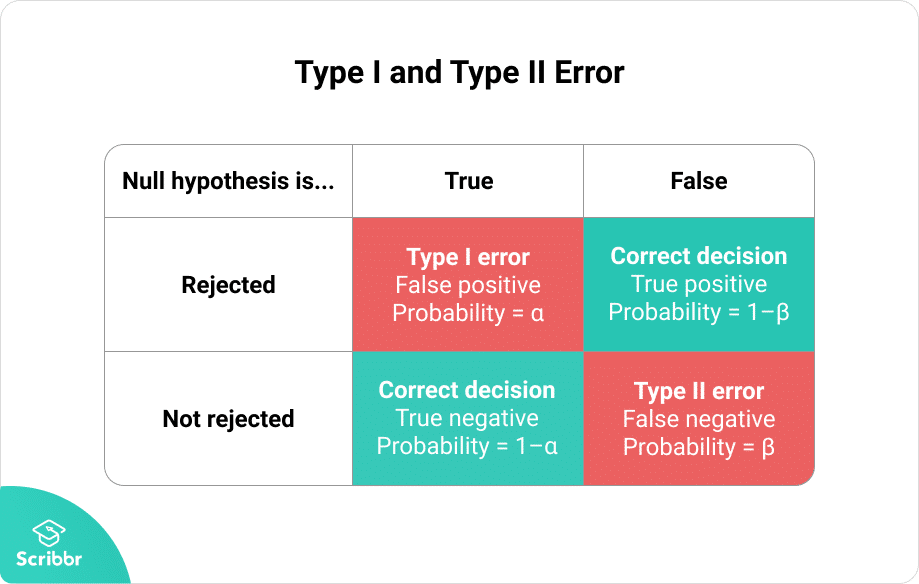
两类错误
- I类错误 当H0正确时,拒绝了H0所犯的错误,也叫错误、弃真错误,其概率为;指研究者得出处理有效应的结论,而实际上并没有效果,“无中生有”。
- II类错误 当H1正确时,接受了H0所犯的错误,也叫错误、取伪错误,其概率为;指假设检验未能侦测到实际存在的处理效应,“失之交臂”
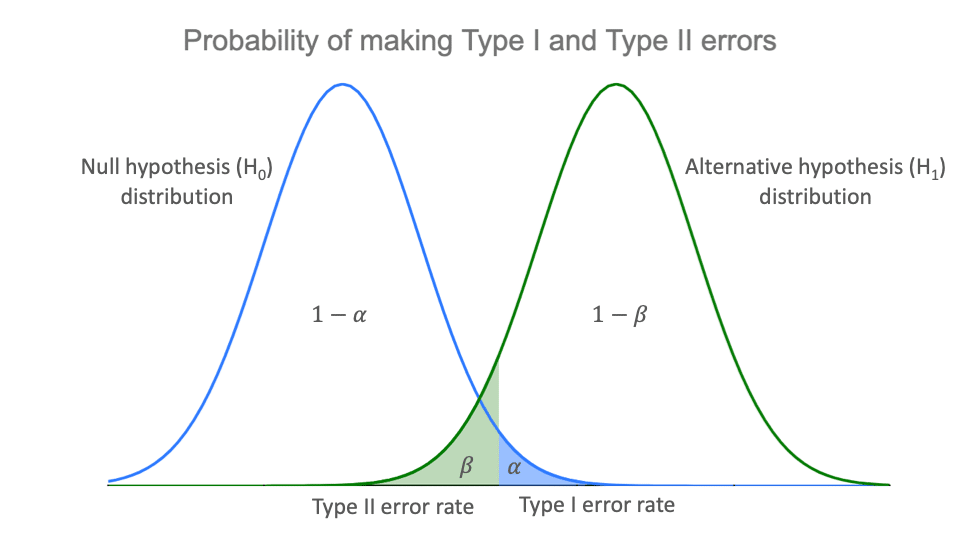
两类错误的关系
- 因为与是在两个相互对立的前提下的概率,所以
- 在其他条件不变的情况下(只移动水平),与不可能同时减小或增大。
- 当样本量增大时,标准误减小,两个分布都更加陡峭,和同时减小
统计检验力
- 某个检验能够正确拒绝一个虚无假设(H0)的概率,其反映正确辨别真实差异的能力,用表示
- 影响因素
- 处理效应 处理效应越明显,越容易被检测,统计检验力越大
- 显著性水平 增大,则相应减小,所以增大,即拒绝虚无假设的概率增大,统计检验力增大。
- 检验的方向性 单侧检验的统计检验力高于双侧检验
- 样本容量 样本容量越大,标准误越小,样本分布均值越集中,统计检验力越大。
两类检验
- 单侧检验
- 强调某一方向的检验如,是否显著“大于”、“优于”等。如
- 双侧检验
- 只强调差异不强调方向的检验,如是否有显著差异。如