样本分布
含义
- 又称抽样分布,以样本统计量为数据构成的分布。
- 设存在某总体
- 从中抽取样本量为的样本
- 计算其平均数、样本标准差等统计量
- 重复2, 3步无数次
- 样本量为n的样本平均数和样本标准差组成的分布即是样本分布。
- 谈论样本统计量时,首先要保证各个样本彼此独立,各个样本都服从同样的分布——采用随机抽样的方法。
样本平均数的分布
- 总体正态,方差()已知时,成正态分布
- 样本分布的平均数
proof
- 样本分布的方差
proof
- 样本分布的标准差(也称为标准误)
- 样本分布的平均数
- 总体非正态,方差()已知,样本容量足够大()时,近似正态分布
- 样本分布的平均数
- 样本分布的方差
- 样本分布的标准差(也称为标准误)
- 总体正态,总体方差未知时,呈t分布
- 样本分布的平均数
- 样本分布的标准差(标准误)
proof 是总体方差的无偏估计
- 总体非正态,总体方差未知,样本量足够大()时,呈近似t分布
- 样本分布的平均数
- 样本分布的标准差(标准误)
t分布
- t分布的形态与无关,与有关
- t分布中,自由度
特点
- 以平均值为0左右对称,左侧t为负值,右侧为正直
- 变量取值
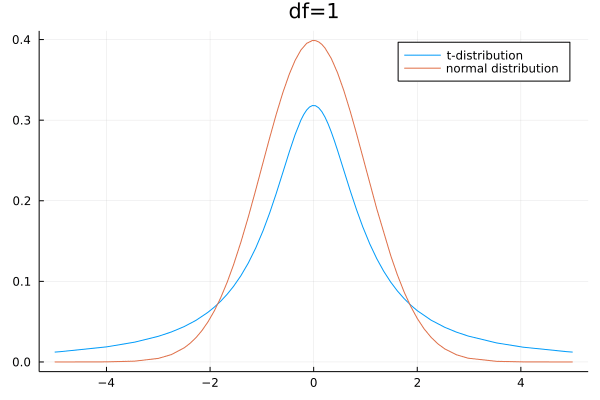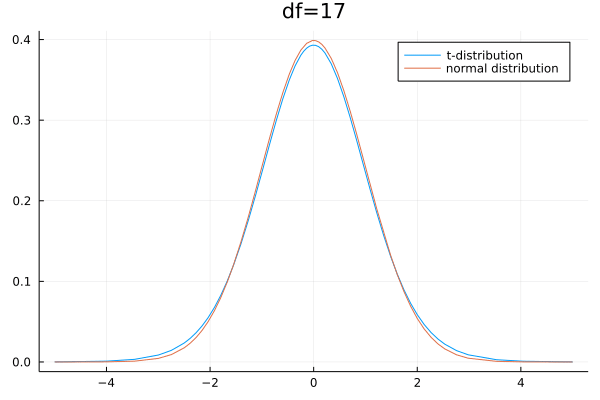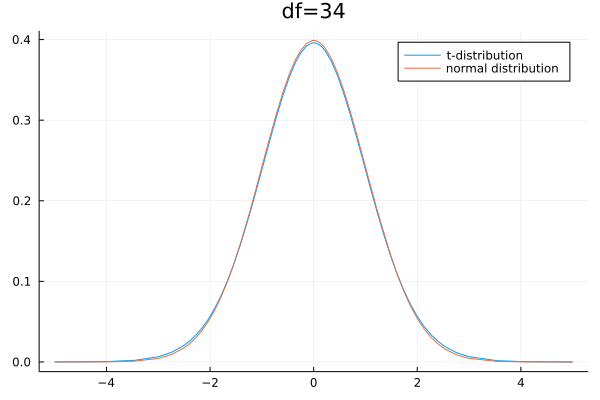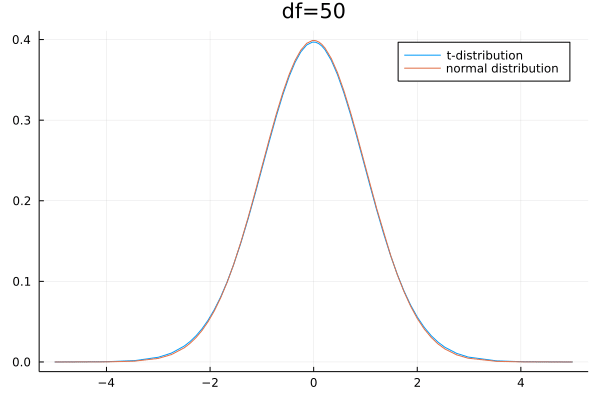
- 样本容量趋于时,t分布接近正态分布,
- 当时,t分布接近正态分布,
- 当时,t分布与正态分布相差较大,
- 随减小,离散程度增大,分布图中间变低尾部变高
t表
方差和标准差的样本分布
- 总体正态,样本容量足够大(),呈正态分布。
- 样本分布的平均数
proof
- 标准差分布的标准差
- 标准差分布的方差
- 样本分布的平均数
分布
- 含义
- 设存在某总体
- 从中抽取样本量为的样本
- 计算样本各值的平方和
- 重复2和3步无数次
- 无数个构成的分布即为分布
- 如果将原始值换为值,同样符合分布
- 总体未知时,用样本均值估计
特点
- 一族正偏态分布。越小,分布越偏;很大时,接近正态分布;,即为正态分布。
- 都是正值
- 分布的和依然是分布,因此,分布具有可加性
- 如果,分布,
- 是连续性分布,但是有些离散型分布也接近分布。
F分布
- 若抽样来自一个总体,
- 因此
特点
- 正偏态分布
- 分布曲线随着分子分母自由度的不同而变化
- 随着和增加,逐渐趋向正态分布
- 总是正值
- 分子自由度为1时,F值与分母自由度相同的概率的t值(双尾概率)的平方相等。